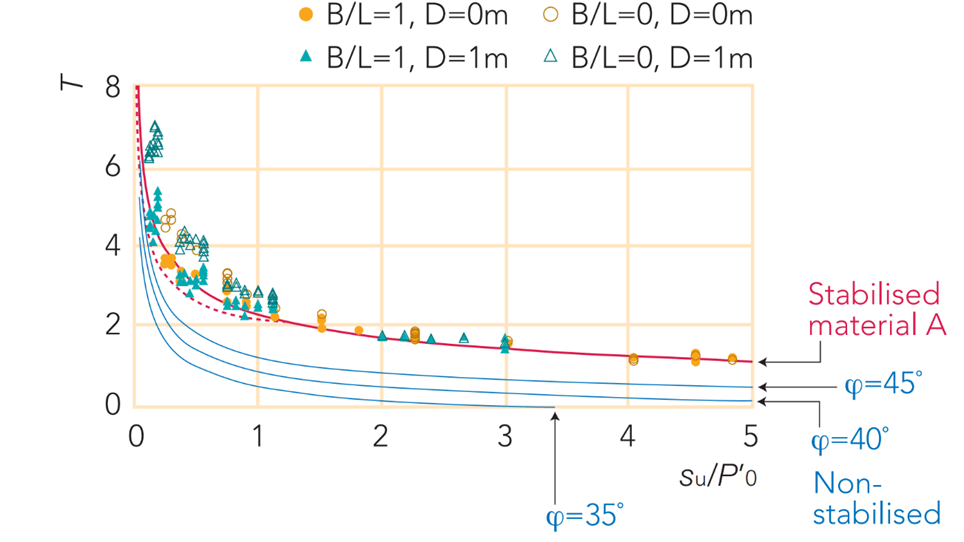Piling is an essential aspect of the construction process for structures over weak soils, without which many large structures would eventually fail. But the equipment used to install pile foundations also needs its own support, particularly in cases where the ground is insufficiently strong – and this is where piling mats come in.
This guide explains how to design a piling mat that’s suitable for your next construction project. As well as exploring the various criteria that should be covered by your piling mat specifications, we’ll take a look at the design methods you can use to calculate all of the key details.
Read on to learn about:
Looking for an answer fast? Use the links above to navigate to the right section. Or if you’re ready to get started with designing piling mats right away, head over to our free software tool, Tensar+, and we’ll help you determine the required specifications in just a few minutes.
A piling mat is a type of working platform that provides a stable surface to support piling rigs, allowing this heavy machinery to be operated safely.
All piling mats consist of a layer of granular fill material that is sufficiently wide, thick, and stable to safely support the operation of piling rigs, and also the movement of this equipment around the site. However, the exact design of a piling mat will vary depending on the loading conditions and requirements of the project.
Piling rigs are tall, heavy machines that are, by their very nature, potentially unstable on a sloping surface. It’s therefore important that they have a strong piling mat to support them, especially when working over ground that is relatively weak. Without a sufficiently stable piling mat, the ground beneath the piling rig may undergo excessive and uneven settlement, with potentially catastrophic consequences for the rig and the workforce.
Piling mats are typically constructed using a well-graded granular material such as crushed rock or clean-crushed concrete, taking into account the compaction and drainage characteristics required. When determining the specifications for a piling mat, engineers also consider:
As we’ve already touched on, piling mats will be made from well-graded stone, crushed hard rock, or clean-crushed concrete. Equally, recycled demolition material can be used to construct piling mats provided that it is sufficiently well graded, with all wood and metal debris removed. Wherever site-won re-cycled materials can be used, this reduces the overall cost and the carbon emissions of a project.
When preparing piling mat specifications, the required thickness is a key dimension that must be carefully determined. The working platform must be sufficiently thick to ensure that the bearing capacity of the overall platform and subgrade is high enough to support the loading regime, including piling rigs, cranes, and all other equipment.
Below, we’ll explore a reliable design approach that can be used to determine how thick the piling mat must be.
It is important that the piling mat extends beyond the working width of the piling rigs. Under normal circumstances, the edges of the piling mat will go beyond the outer pile positions by 2m or more. This needs to be considered and specified as part of the piling mat design.
In the UK, the piling contractor will require a ‘Working Platform Certificate’, signed by the Principal Contractor, confirming that the platform has been properly designed for the specific loading and ground conditions on site, constructed in accordance with the design, and will be regularly and adequately maintained throughout use.
Piling mat design should be carried out by a competent person, preferably a geotechnical engineer. The design will be influenced by the ground conditions and groundwater regime. A ground investigation must therefore be first carried out covering the entire area of the piling mat. The final design thickness will depend upon the bearing capacity of the subgrade, the piling mat fill material, and the expected piling rig and other loading.
There has been some dissatisfaction in the construction industry with the design methods used for piling mats: the calculation methods are quite empirical and use imprecise input parameters, while other methods involve the use of multiple design charts, and most result in an overly conservative piling mat thickness. This generates higher than necessary costs for the Principal Contractor. In response, Tensar developed a new design method for piling mats that addresses all of these concerns: the T-Value method. T-value represents the load transfer efficiency of a granular layer.
Importantly the T-value method enables the designer to correctly use an improved load transfer efficiency for a granular layer incorporating a stabilisation geogrid. This typically results in significant reductions in piling mat thickness with the cost saving and environmental benefit that delivers.
Read more about the T- value method lower down this page.
Tensar has incorporated the T-value method for design of piling mats into Tensar+® software. This software is available free of charge from Tensar. It is easy to use by a competent geotechnical engineer.
Two design options are available: Working Platform and Tracked Plant. The second of these follows the requirements of BR470:2004 plus the guidelines of the BRE guidelines. This is the more appropriate option for piling mat design.
Figure 1 - Tensar+ offers two design options
Selecting the Tracked Plant option opens the design page. Load conditions can be input for each of the two load cases defined in BR470, together with the appropriate factors of safety for each. Next, the piling mat fill material properties can be entered. Finally, the subgrade characteristics and ground water conditions are entered.
Figure 2 - Tensar+ Design page for input of loads, materials, and subgrade conditions
The design calculation is live. As data is input, required piling mat thicknesses for the stabilised and non-stabilised options are displayed graphically. For the stabilised case, the required geogrid type(s) and vertical spacing are displayed.
Value Calculation – A second tab opens a Value page. Typical material and geogrid costs are included by default but these can be changed by entering project specific materials costs. The designer can then identify the total costs for each option and the savings between stabilised and non-stabilised options. The costs and savings calculated and displayed are the construction cost and environmental cost, together with construction time.
Figure 3 - Tensar+ Value calculation page
A further tab displays design specific specification documents that can be incorporated into project documents.
Tensar+ software is cloud based and may be accessed from PC’s or mobile devices. Completed designs can be stored and downloaded in pdf. format for retention by the designer.
Tensar’s design approach, the T-Value method, is based on the non-dimensional relationship between bearing capacity and the load transfer efficiency of a granular layer, expressed as a dimensionless T-value. This is dependent on the shear strengths of the granular layer and the subgrade beneath. T-value for a specific aggregate type (and geogrid type for stabilised aggregates), is derived from numerical analysis, parametric study, and physical testing.
The T-value method has been rigorously validated and published in peer reviewed papers.
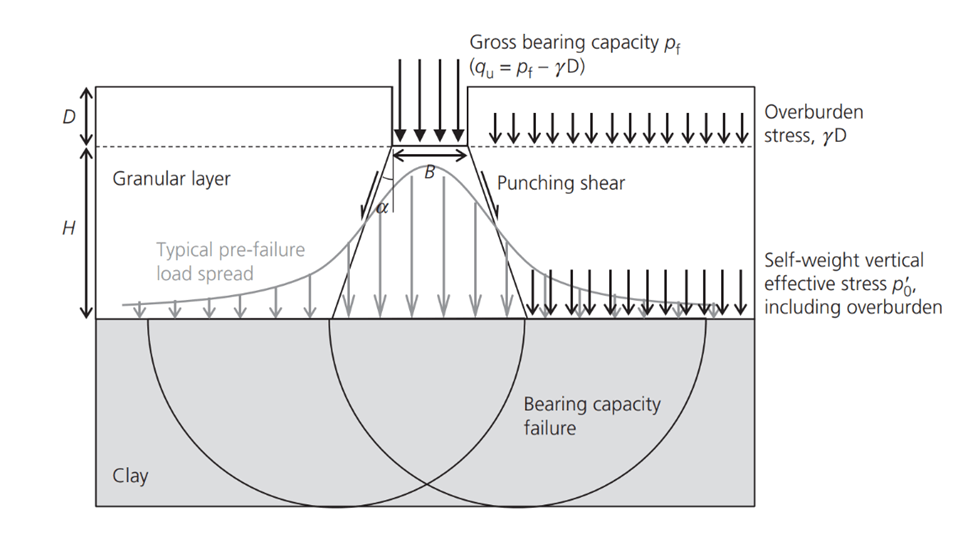
Figure 4 Geometry of the problem (Lees 2020)
A piling mat comprises a granular layer over a weaker subgrade soil, in this case, clay (Figure 4). The design must determine the required thickness of the granular layer to satisfy each load case. BR470 defines two critical loading conditions that must be examined for the specific piling rig being considered.
The T-value for non-stabilised granular material can be calculated or obtained from a chart (Figure 5). The three blue lines are T-value curves for different friction angles. A single T-value curve for a specific geogrid stabilised granular material is also shown on the chart in red. Different stabilisation geogrids will have similar but different T-value curves. Tensar has developed T-value curves for a range of their geogrids in a variety of granular materials.
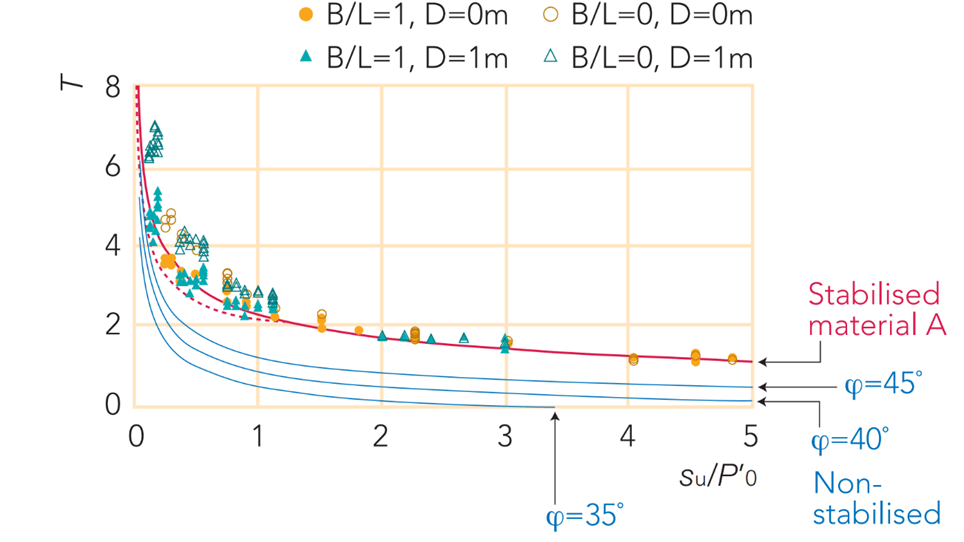
Figure 5 - T-Value variation with su undrained shear strength of clay, for non-stabilised granular layers (blue) and a stabilised layer with a specific geogrid (red). (Lees & Matthias 2019)
Having determined the T-value, the two simple equations below in Figure 6, enable calculation of bearing capacity ratio for a strip footing (B/L = 0) and a square footing (B/L = 1), where B is the footing width and B the length.
Piling rigs have a rectangular footing where B is the track width and L is the effective length of track applying pressure. The effective track length L and pressure distribution is defined for each load case.
The bearing capacity ratio for a rectangular footing is obtained by linear extrapolation between the strip footing (B/L = 0) and square footing (B/L=1).
The inequalities in the two equations in Figure 3 are needed to check for cases where critical shear failure occurs entirely within the granular layer.
Figure 5 - Bearing capacity equations for strip and square/circular footings, where T represents the load transfer efficiency of the granular layer, qs=surface bearing capacity of subgrade when H=0, qg = surface bearing capacity of granular layer when H=infinite. (Lees 2020)
Keen to learn more about applying this method to piling mat design? Take a look at our dedicated T-Value guide.
This guide has explained how to determine the piling mat specifications for your next construction project. By following the T-Value piling mat design process outlined above, you’ll be able to create a working platform that is stable enough to support your piling rigs without being overengineered for the task at hand.
See our T-Value guide for further information on applying this method to piling mat design. If you’re looking for extra support with your project, sign up for our free software Tensar+ and navigate to the working platform design module.
What our new Tensar+ training video on our Tracked Plant module here.
